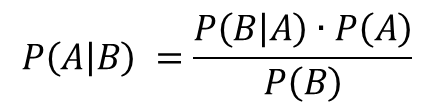Artikel:Bayes-Formel

Die Bayes-Formel dient der Berechnung von bedingten Wahrscheinlichkeiten. Das ist die Wahrscheinlichkeit für den Eintritt eines Ereignisses B unter der Bedingung, dass das damit verknüpfte Ereignis A bereits eingetreten ist.

mit

P(A│B): Wahrscheinlichkeit für Ergebnis A, wenn B eingetreten ist.

P(B│A): Wahrscheinlichkeit für Ergebnis B, wenn A eingetreten ist.

P(A): Wahrscheinlichkeit für Ergebnis A

P(B): Wahrscheinlichkeit für Ergebnis B

Geschichte

Die Bayes-Formel wurde von dem englischen Mathematiker Thomas Bayes (~1701-1761) in dem nach seinem Tod veröffentlichten Aufsatz „An Essay Towards Solving a Problem in the Doctrine of Chances“ beschrieben.

Anwendung

In der Medizin wird die Bayes-Formel u. a. benötigt, um zu beurteilen, wie weit eine Ausgangswahrscheinlichkeit durch weitere Informationen (wie zum Beispiel ein durchgeführter Test oder ein neues Studienergebnis) modifiziert werden muss. Ganz konkret wird das, wenn ein Patient auf eine bestimmte Krankheit getestet wird und ein positives Ergebnis erhält: Wie wahrscheinlich ist es, dass dieser Patient die Krankheit tatsächlich hat?

Beispiel

Wenn man also durch langjährige Beobachtung weiß, dass 1% der Bevölkerung eine bestimmte Krankheit hat (Ereignis A: Wahrscheinlichkeit für jeden Bürger 1%), und wenn man einen Test hat, der mit 90%iger Sicherheit (Ereignis B: Wahrscheinlichkeit 90%) anzeigt, ob eine bestimmte Person diese Krankheit hat: Wie hoch ist dann die Wahrscheinlichkeit, dass diese positiv getestete bestimmte Person diese Krankheit tatsächlich hat?

Lösung

Ereignis A sei, die Krankheit liegt vor und Ereignis B, der Test zeigt die Krankheit an. Gesucht ist die Wahrscheinlichkeit P(A│B), also dass der Patient tatsächlich die Krankheit (Ergebnis A) hat, wenn der Test angeschlagen hat (Ereignis B).

• Die Wahrscheinlichkeit P(B│A) für ein (korrektes) Ergebnis des Tests, falls die Krankheit vorliegt, ist vorgegeben als 90%.
• Die Wahrscheinlichkeit P(A) für das Vorhandensein der Krankheit vor Durchführung des Tests ist aber nur 1%.
• Die Wahrscheinlichkeit P(B), dass der Test positiv ausfällt, setzt sich aus den beiden Wahrscheinlichkeiten zusammen:
  • Erstens: Der Patient hat die Krankheit und der Test erkennt das korrekt: 0,01 x 0,9
  • Zweitens: Der Patient hat die Krankheit nicht, aber der Test zeigt fälschlicherweise doch die Krankheit an: 0,99 x 0,1
  • Zusammen: P(B) = (0,01 x 0,9) + (0,99 x 0,1) = 0,009 + 0,099 = 0,108

Durch Einsetzen in die Bayes-Formel erhält man die Wahrscheinlichkeit, dass der Patient bei einem positiven Testresultat die Krankheit tatsächlich hat.

P(A│B) = P(B│A) x P(A) / P(B) = 0,9 x 0,01 / 0,108 = 0,083 = 8,3%

Mit anderen Worten: Es mag sein, dass der Test zu 90% zuverlässig ist. Man weiß zwar, dass nur 1% der Bevölkerung die Krankheit haben, aber man weiß nicht vorher, ob ein bestimmter Patient, der gerade getestet wird, die Krankheit hat.

Diskussion

Das Ergebnis scheint erst einmal der Intuition zu widersprechen, da man bei einem zu 90% zuverlässigen Test auch ein ähnlich zuverlässiges Ergebnis erwartet. Ebenso ist nicht unmittelbar verständlich, warum hier die Häufigkeit des Auftretens der Krankheit (A) die Zuverlässigkeit des Testergebnisses (B) beeinflusst. Selbst unter Ärzten scheinen Fehler beim Beurteilen solcher Wahrscheinlichkeiten häufig vorzukommen; nach D. M. Eddy schätzten in einer Studie 95 von 100 Ärzten die Wahrscheinlichkeit für das Vorliegen der Krankheit grob falsch ein (auf > 50%).

Verständlich wird das aber, wenn man bedenkt, dass nicht nur die (wenigen) erkrankten Personen getestet werden, sondern auch (viel mehr) Gesunde. Die Mehrheit der Tests mit dem Ergebnis „krank“ gehen eben nicht auf richtig diagnostizierte kranke Personen zurück, sondern darauf, dass bei den vielen Tests an Gesunden eine entsprechende Zahl von falschen Ergebnissen produziert wird.

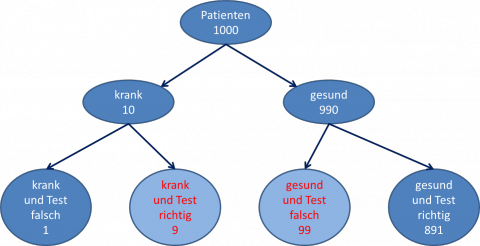
Gezeigt wird dies im obenstehenden Diagramm an einem Beispiel mit 1000 Patienten.

Die Wahrscheinlichkeit dafür, dass ein Testergebnis „krank“ korrekt die Krankheit anzeigt, ergibt sich aus der Zahl der Kranken mit korrektem Test im Verhältnis zu allen Tests mit dem Ergebnis „krank“:

P(A│B) = 9 / (9+99) = 0,083 = 8,3%

Die absolute Anzahl der korrekt positiven Testergebnisse ist also bei diesen (nicht untypischen) Zahlenverhältnissen viel geringer als die Anzahl der falsch positiven Resultate. Daher ist die Wahrscheinlichkeit, dass der Patient die Krankheit tatsächlich hat, auch bei einem positiven Testbefund unerwartet gering.

Bezug zur Homöopathie

Dasselbe Problem tritt auch auf, wenn man Hypothesen prüft, die z.B. aufgrund von widersprechenden Grundlagenexperimenten oder bereits vorhandenen negativen Studien a priori unwahrscheinlich sind (Wahrscheinlichkeit A ist gering). Oder wie die Statistikprofessorin Regina Nuzzo dazu prägnant sagte:

Je unplausibler die Hypothese - denken Sie an Telepathie, Aliens, Homöopathie -, desto höher ist die Wahrscheinlichkeit, dass sich ein aufregender Befund als Fehlalarm entpuppt.

Prüft man also eine solche Hypothese mit dem in medizinischen Studien häufig benutzten Signifikanzniveau von mindestens 95% (Irrtumswahrscheinlichkeit < 5%), dann muss man ähnlich wie im Anwendungsbeispiel erwarten, dass die überwiegende Zahl der positiven Studienergebnisse falsch ist und auf der Fehlerwahrscheinlichkeit der Studie beruhen. In diesem Fall kann eine Analyse mittels der Bayes-Formel besser über die Aussagekraft der Studie informieren als die ausschließliche Angabe der statistischen Signifikanz.

Quellen- und Literaturangaben