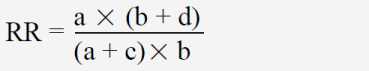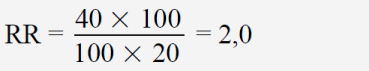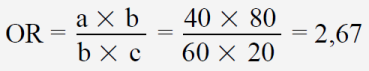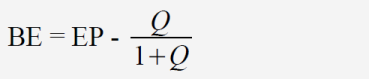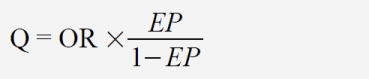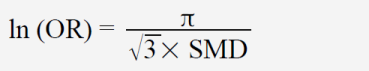Effektstärke

In diesem Artikel wird die Effektstärke behandelt, wie sie zur Bewertung des Ergebnisses einer klinischen Studie angewendet wird. Im Gegensatz zur Signifikanz, die die Wahrscheinlichkeit für das Zustandekommen mindestens des beobachteten Unterschieds (etwa zwischen Verum- und Kontrollgruppe) bewertet, ist die statistische Effektstärke ein Maß dafür, wie groß dieser Unterschied ist. Für die Angabe der Effektstärke werden unterschiedliche Maßzahlen verwendet. In diesem Artikel wird die Bedeutung und die Interpretation der verschiedenen Zahlenwerte behandelt, besonders im Hinblick darauf, was sie zum Nutzen der in einer Studie getesteten Therapie für die Patienten aussagen.

Allgemeines

In klinischen Studien wird die Effektstärke eher selten dargestellt. In systematischen Reviews und Meta-Analysen hingegen werden die im Folgenden beschriebenen Kennzahlen häufig benutzt. Die Autoren solcher Arbeiten müssen unterschiedliche Ergebnisse aus mehreren Studien zusammenfassen, die jeweils verschiedene Kriterien und Maßstäbe anwenden. Hierfür ist es erforderlich, aus den Daten der betreffenden Studien je eine Kennzahl zu ermitteln, die das Ergebnis charakterisiert, dabei allerdings unabhängig von den Maßeinheiten ist. Diese Effektstärke genannte Kennzahl muss im Rahmen einer Meta-Analyse aus den Studiendaten ermittelt werden. Auch die Ergebnisse der Meta-Analyse werden als zusammengefasste Effektstärke dargestellt, woraus sich die Notwendigkeit ergibt, diese Angaben zu interpretieren und zu bewerten.

Dieser Artikel beschränkt sich auf die in medizinischen Meta-Analysen üblichen Maßzahlen und den Definitionen, wie sie im Cochrane-Handbuch, Kapitel 9, für systematische Reviews aufgeführt sind, und bezieht sich, wenn nicht anders angegeben, auf diese Quelle.

Definition

Die Effektstärke ist eine dimensionslose statistische Kennzahl für die Größe eines in einer vergleichenden Untersuchung aufgetretenen Effekts. Es handelt sich dabei um eine reine statistische Größe, die für sich betrachtet nur wenig zum tatsächlich beim Patienten fühlbaren therapeutischen Effekt und dessen Relevanz für das untersuchte Krankheitsgeschehen aussagt.

Effektstärke und Signifikanz

Die Effektstärke ist ein Maß für die Größe eines aufgetretenen Effekts. Die im Zusammenhang mit Einzelstudien viel häufiger zitierte Signifikanz hingegen ist ein Maß für die (Un-)Wahrscheinlichkeit, dass das Ergebnis aufgetreten wäre, wenn die Nullhypothese zuträfe. Im allgemeinen Sprachgebrauch wird zwar mit einem „signifikanten Ergebnis“ eine große Effektstärke assoziiert, aber der Zusammenhang zwischen Signifikanz, also dem P-Wert, und der Effektstärke ist nur recht indirekt. Ein Ergebnis mit großer Effektstärke ist in einer Studie weniger wahrscheinlich und daher von stärkerer Signifikanz als bei kleiner Effektstärke. Dies lässt sich aber nicht auf den Vergleich zweier Studien übertragen: Wird eine Studie nur mit einer eher niedrigeren Teilnehmerzahl durchgeführt, führt erst eine hohe Effektstärke zu einem signifikanten Ergebnis, wohingegen bei hohen Teilnehmerzahlen schon bei kleinen Effektstärken signifikante Ergebnisse auftreten.

→ siehe auch Hauptartikel Statistische Signifikanz

Effektstärke und therapeutische Relevanz

Ein Umstand, der bislang in der Literatur wenig Beachtung findet, liegt auch darin, dass die Effektstärke ein reines statistisches Maß ist und nur sehr indirekt mit der therapeutischen Relevanz korrespondiert. Ein Patient, der sich einer Behandlung unterzieht, erwartet eine für ihn fühlbare Verbesserung seines Befindens, und zwar in realen absoluten Größen. Die meisten Maßzahlen zur Effektstärke stellen jedoch eine relative Bewertung dar, zu deren Interpretation weitere Informationen aus den statistischen Daten erforderlich sind. Der aufgetretene Unterschied wird als stark, mittel oder schwach bewertet, je nachdem wie stark er sich in den Streuungen der gemessenen Daten abzeichnet.

Die Effektstärke ist also ein rein statistisches Maß, das angibt, wie stark unterschiedlich ein von den Autoren einer Arbeit festgelegtes Kriterium in beiden Gruppen ausgeprägt ist. Auf die therapeutische Bedeutung des Studienergebnisses kann man folglich nur durch eine gemeinsame Betrachtung von Effektstärke und Bewertungskriterium schließen. Wenn beispielsweise eine kleine Änderung als Zielkriterium gewählt wurde („Gewichtsreduktion um mindestens 0,1 kg“) und viele Patienten das in der einen Gruppe erreichen und in der anderen nicht, ist dies zwar ein starker statistischer Effekt, aber nur ein kleiner Therapiegewinn, wie jeder, der mit Gewichtsproblemen zu tun hat, wohl weiß.

Andererseits kann auch eine kleine Effektstärke zu einer für den Betroffenen wertvollen Therapie führen. Man denke an unheilbare Krankheiten wie Diabetes I; da wären schon kleinste Heilungsraten ein großer Fortschritt.

Anwendung

In einer als Vergleichsstudie angelegten klinischen Untersuchung wird die Wirkung einer Therapie oder einer Arznei untersucht, indem zwei Vergleichsgruppen gebildet werden, deren eine, die Verumgruppe, die zu prüfende Arznei erhält, die andere, die Kontroll- oder Placebogruppe, ein nicht unterscheidbares Placebo. Der Effekt zeigt sich darin, dass sich Unterschiede zwischen den beiden Gruppen ergeben, die wahrscheinlich nicht durch einen Zufall verursacht worden sind. Je nachdem, welcher Art die betrachteten Daten sind, sind verschiedene Verfahren und Maßzahlen zur Bewertung der Effektstärke in Gebrauch.

Dichotome Daten

Dichotome Daten liegen vor, wenn die Probanden je nach Ergebnis in zwei Kategorien eingeteilt werden (z.B. geheilt vs. nicht geheilt oder Erfolg vs. kein Erfolg). Jeder Patient wird einer dieser Kategorien zugeordnet. Der Behandlungserfolg zeigt sich dann darin, dass in der Verumgruppe der Anteil der Patienten mit dem positiven der beiden Merkmale größer ist als in der Kontrollgruppe. Die Therapie wird folglich danach bewertet, wie wahrscheinlich es ist, dass sich beim Patienten das positive Merkmal einstellt.

Typischerweise können die Ergebnisse in einer Kontingenztafel (auch Kreuztabelle genannt) dargestellt werden wie in diesem fiktiven Beispiel, das für die folgenden Betrachtungen herangezogen wird:

	Verumgruppe	Kontrollgruppe	Summe
Erfolg	40 (= a)	20 (= b)	60 (= a+b)
kein Erfolg	60 (= c)	80 (= d)	140 (= c+d)
Summe	100 (= a+c)	100 (= b+d)	200 (= a+b+c+d)

Die Bedeutung leuchtet unmittelbar ein: Von der Verumgruppe haben 40 der 100 Patienten einen Erfolg erzielt, von der Placebogruppe nur 20 von 100, was für eine Wirkung der Therapie spricht, da dies ein signifikantes Ergebnis darstellt, wie sich mit einem Signifikanztest zeigen lässt.

Risk Difference (RD)

Auch wenn man den erwünschten Effekt einer Heilung sprachlich besser als „Chance“ bezeichnen würde, hat sich in der Statistik das Wort „Risiko“ (Risk) für diesen Sachverhalt eingebürgert und verbreitet. Wir bleiben deshalb wegen der Konsistenz zur veröffentlichten Literatur ebenfalls bei diesem Begriff.

Das Risiko ist die Anzahl der erfolgreichen Fälle im Verhältnis zur Gesamtzahl der Teilnehmer in der Gruppe. Für Verum- und Kontrollgruppe wären dies a/(a+c) bzw. b /(b+d), also die Zahlenwerte 0,4 (40 %) bzw. 0,2 (20 %). Die Effektstärke als Risk Difference („Risikodifferenz“) ergibt sich dann als die Differenz 0,4 minus 0,2 zu 0,2.

RD kann maximal den Wert 1 erreichen, was allerdings nur ein hypothetischer Fall ist, denn dazu dürfte in der Placebogruppe niemand einen Erfolg zeigen, mit Medikament jedoch alle Teilnehmer. Dies ist selbst bei den besten Therapien sicher nicht der Fall. RD = 0 bedeutet, dass keine Veränderung der Verumgruppe gegen die Konrollgruppe aufgetreten ist, RD < 0 zeigt hingegen einen Nachteil der Therapie an.

Interpretation

Dieser Zahlenwert lässt sich leicht interpretieren: RD ist der Anteil (oder der Prozentsatz) der Patienten, die von der Behandlung profitiert haben. Die Placebogruppe zeigt im obigen Beispiel, dass 20 % der Patienten auch ohne Arznei genesen. Da mit Arznei bei 40 % der Patienten ein Erfolg eintritt, profitieren in diesem Beispiel 20 % der Patienten der Therapiegruppe von der Behandlung, die anderen 80 % tun das nicht. (Allerdings werden alle 40 % der erfolgreich therapierten Patienten sehr wahrscheinlich davon überzeugt sein, sie wären wegen der Einnahme der Arznei gesund geworden.)

Damit stellt RD die Wahrscheinlichkeit dar, mit der ein Patient infolge der Therapie den als Zielkriterium definierten Erfolgsfall erreichen kann. Je größer diese Zahl ist, desto sicherer kann ein einzelner Patient mit einem Nutzen rechnen. Obwohl RD also eine sehr anschauliche und leicht zu verstehende Größe ist, wird sie anscheinend nur relativ selten angewendet. Keine der großen Meta-Analysen zur Homöopathie und keine der üblicherweise zitierten vermeintlich erfolgreichen klinischen Studien verwendet diese Kennzahl. Man könnte zu dem Verdacht kommen, dass dies daran liegt, dass die Zahlenwerte vergleichsweise niedrig sind, nämlich deutlich unter Eins liegen würden.

Number needed to treat (NNT)

Praktisch die gleiche Aussagekraft wie RD hat die im englischen Sprachraum gelegentlich verwendete Kennzahl Number needed to treat („für eine erfolgreiche Behandlung nötige Anzahl“). Dies ist einfach der Kehrwert von RD, im obigen Beispiel mit RD = 0,2 also 5. Es müssen fünf Patienten behandelt werden, damit ein Patient (mehr als unter Placebo) erfolgreich geheilt wird. Je niedriger NNT, desto größer ist die festgestellte Effektstärke der Behandlung.

Risk Ratio (RR)

Wenn man die „Erfolgsrisiken“ der beiden Gruppen nicht subtrahiert, sondern ins Verhältnis setzt, dann erhält man als eine andere auch eher selten gebräuchliche Kennzahl die Risk Ratio („Risikoverhältnis“), auch als Relative Risk („relatives Risiko“) bezeichnet. In der obigen Kontingenztafel wäre das

Dabei wird der Quotient zumeist so gebildet, dass ein Wert über 1 einen Vorteil für die Therapie bedeutet. Für das obige Beispiel ergibt sich

RR kann alle Zahlenwerte zwischen Null und Unendlich annehmen und hat nur einen eindeutig interpretierbaren Wert, nämlich RR = 1. Dieser bedeutet, dass das Risiko in beiden Gruppen gleich ist, also kein Effekt aufgetreten ist. Ansonsten gibt es keine obere Grenze: Wenn der Wert für die Placebogruppe sehr klein ist, für die Arzneigruppe jedoch recht hoch, können beliebig große Zahlen auftreten. Eine intuitive Bewertung, ob es sich bei einem bestimmten RR um einen großen oder kleinen Effekt handelt, das heißt, ob viele oder nur wenige Patienten davon profitieren, ist kaum möglich.

Auf der anderen Seite können keine negativen Werte auftreten. Negative Ergebnisse, bei denen die Verumgruppe schlechter abgeschnitten hat als die Placebogruppe, ergeben Werte zwischen 0 und 1, und positive Ergebnisse zeigen sich in Werten zwischen 1 und „unendlich“. Dies ergibt für eine intuitive Erfassung der Sachlage die Schwierigkeit, dass die Kennzahl deutlich nicht-linear ist. Wenn sich bei einem Versuchsergebnis ein Vorteil RR = 5 ergeben würde, dann wäre das genaue Gegenteil davon, also ein ebensogroßer Nachteil, durch den Kehrwert RR = 1/5 = 0,2 gekennzeichnet. Da 0,2 deutlich näher bei 1 liegt als 5, werden in zahlenmäßigen Gegenüberstellungen von Studienergebnissen auf diese Weise positive Resultate überbetont. Bei grafischen Darstellungen wird daher der Logarithmus der Risk Ratio aufgetragen, womit diese Nachteile vermieden werden. Ein neutrales Ergebnis zeigt sich bei log(RR) = 0, negative führen zu Zahlenwerten unter 0, positive zu Werten über 0.

Interpretation

Die Interpretation einer als RR gegebenen Effektstärke wird dadurch erschwert, dass man eine zweite Angabe braucht, um sich ein Bild vom Ergebnis der Studie machen zu können. Erst wenn man weiß, wie groß der Anteil der erfolgreichen Patienten in der Placebogruppe war, kann man die Erfolgsrate in der Therapiegruppe bestimmen.

Man kann aus RR aber immerhin noch ablesen, dass die Wahrscheinlichkeit, infolge der Therapie einen Erfolg zu erzielen, um den Faktor RR höher ist als ohne Therapie. Man weiß bei RR = 3, dass man mit der Therapie die dreifache Chance auf Erfolg hat, nur eben nicht, ob sich die Erfolgsaussichten von 1 auf 3 % erhöht haben oder von 20 auf 60 % (was ein RD von 2 % bzw. 40 % ergäbe).

Odds Ratio (OR)

Bei der Odds Ratio wird das Verhältnis der „Odds“ gebildet, die eine Größe darstellen, die im deutschen Sprachraum außerhalb der Statistik völlig ungebräuchlich ist. Daher ist die oftmals anzutreffende Bezeichnung „Quote“ bzw. „Quotenverhältnis“ für Odds Ratio etwas irreführend. Eine Frauenquote oder eine Erwerbsquote bezeichnen beispielsweise den Anteil der Frauen in der Gesamtgruppe der Führungskräfte bzw. der Erwerbstätigen an der Gesamtbevölkerung. Unter Odds wird im englischen Sprachraum hingegen das Verhältnis des einen Anteils zum anderen bezeichnet.

In obigem Beispiel wäre das Risiko in der Arzneigruppe 40/100 = 0,4, die Odds hingegen 40/60 = 0,667.

Die Odds Ratio ergibt sich für das obige Versuchsergebnis zu

Da OR die bei weitem am häufigsten angewendete Kennzahl für die Effektstärke ist, soll diese hier näher betrachtet werden. Es zeigt sich, dass die Odds Ratio bei der Darstellung von Studienergebnissen nicht unproblematisch ist. Sie wäre hingegen vorteilhaft bei Untersuchungen anzuwenden, wenn nur sehr kleine Wahrscheinlichkeiten auftreten, etwa in epidemiologischen Untersuchungen von Krankheiten sehr kleiner Häufigkeiten. Auch hat OR einige mathematische Eigenschaften („Symmetrie“), die dem Fachmann die Arbeit erleichtern. Die Interpretation von Studienergebnissen hingegen ist schwierig und dem Laien kaum möglich.

Eigenschaften

Ebenso wie Risk Ratio hat Odds Ratio eine Reihe von Eigenschaften, die eine intuitive Interpretation erschweren, im Falle der OR jedoch fast unmöglich machen.

Der Wertebereich von OR reicht wie bei RR von Null bis Unendlich, mit 1 als Kennwert für einen nicht eingetretenen Effekt. Zumeist wird OR so gebildet, dass Zahlenwerte über 1 einen Vorteil zugunsten der Therapiegruppe bedeuten. Damit ergibt sich die gleiche Asymmetrie wie bei RR: Während positive Ergebnisse ganz erheblich über 1 liegen können, erscheinen negative Ergebnisse auf den ersten Blick nicht allzu weit unter 1. Auf einer von den meisten Menschen vermutlich intuitiv angenommenen Linearität der Skala würde sich unser Beispiel mit seinem genauen Gegenteil zu 1/2,67 = 0,375 deutlich weniger schlecht ausnehmen als ihm eigentlich zukommt. Somit überzeichnet die Betrachtung von Studienergebnissen anhand der Zahlenwerte von OR die Ergebnisse in die positive Richtung. Bei den Reviews der Cochrane Collaboration wird dies dadurch ausgegelichen, dass in der grafischen Darstellung der Logarithmus von OR aufgetragen wird. Manche Autoren empfehlen statt OR eine „Logit“ genannte Größe zu verwenden, dies wäre der natürliche Logarithmus von OR, also ln(OR).

Da die Werte nach oben unbegrenzt sind und es außer dem Startpunkt OR = 1 keinen anderen aussagekräftigen Festpunkt gibt, ist eine intuitive Bewertung, ob es sich um eine große oder kleine Effektstärke handelt, nicht ohne weiteres möglich. Man vergleiche das mit dem in der Technik üblichen Wirkungsgrad, der das Verhältnis zwischen Nutzen und Aufwand beschreibt. Da dieser Wert nur zwischen 0 und 1 liegen kann, weiß man, dass ein Wirkungsgrad von 0,95 schon recht gut ist und nicht mehr viel Verbesserungspotenzial gegeben ist. Bei OR ist das nicht so. OR lässt überhaupt nicht erkennen, wieviel Potenzial nicht genutzt wurde.

Nichtlinearität von OR

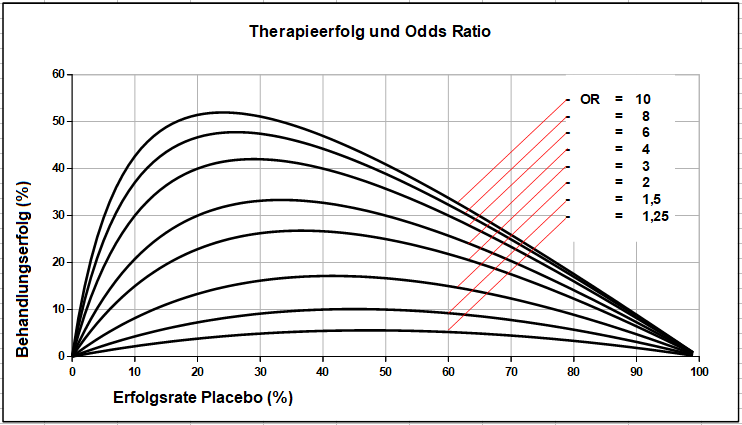
Durch die Verwendung der Odds zur Bildung der Kennzahl ergibt sich ein nichtlinearer Verlauf der Odds Ratio, wie er in der folgenden Grafik dargestellt ist:

Die Erfolgsrate unter Placebo stellt den Anteil der Patienten dar, die unter Placebo die im Zielkriterium festgelegte Verbesserung des Befundes erreicht hatten. Unter dem Behandlungserfolg ist zu verstehen, um wieviel größer der Anteil der erfolgreich behandelten Patienten in der Therapiegruppe ist (= RD). Ablesebeispiel: Für OR = 4 und einer Erfolgsrate unter Placebo von 20 % kann man aus dem Diagramm einen Therapieerfolg von ca. 30 % entnehmen. In der Verumgruppe lag der Anteil der erfolgreich behandelten Patienten um 30 Prozentpunkte höher als unter Placebo, mithin bei 20 + 30 = 50 %.

Die Kontingenztafel für dieses Versuchsergebnis sähe also wie folgt aus:

	Verumgruppe	Kontrollgruppe	Summe
Erfolg	50	20	70
kein Erfolg	50	80	130
Summe	100	100	200

An obigem Diagramm sind einige Schwächen von OR als Kennzahl für Versuchsergebnisse erkennbar:

Die Kennzahl ist stark nicht-linear, das heißt, für kleine Werte von OR bedeutet eine Änderung von OR eine stärkere Zunahme des Behandlungserfolgs als bei größerem OR. Bei einer Placeborate von beispielsweise 20 % bedeutet der Sprung von OR = 2 auf OR = 3 eine Zunahme des Behandlungserfolgs um rund 10 Prozentpunkte, von OR = 9 auf OR = 10 hingegen nur noch knapp 2,5 Prozentpunkte. Wobei sich diese Verhältnisse auch noch abhängig von der Placeborate verändern – und auch das noch nicht homogen: Während bei OR = 4 die Effektstärke mit zunehmender Placeborate zunächst steigt, nimmt sie oberhalb von 30 wieder ab. Und auch der Punkt, an dem für ein bestimmtes OR der maximale Effekt auftritt, verschiebt sich mit wachsendem OR zu kleineren Placeboraten hin.

Die wesentliche Schwäche von OR als Kennzahl liegt aber darin, dass höchst unterschiedliche Versuchsergebnisse den gleichen Kennwert ergeben. Da OR als Verhältniszahl zwei Größen – die Odds der beiden Gruppen – ins Verhältnis setzt, können viele Wertepaare aus zwei Odds den gleichen Zahlenwert ergeben. OR von 4 kann bedeuten, dass bei einer Placeborate von 5 % ein Behandlungserfolg von rund 15 % vorliegt, bei einer Placeborate von 30 % der Behandlungserfolg fast bei 35 %, oder auch, dass bei einer Placeborate von 80 % der Behandlungserfolg bei 15 % liegt.

Daraus folgt ein in der Literatur bislang wenig beachteter Schwachpunkt, der OR als Kennzahl anhaftet, nämlich die Inkonsistenz. An sich müsste es so sein, dass man, wenn man zwei Studienergebnisse mit gleicher Kennzahl zusammenfasst, auch bei dem zusammengefassten Ergebnis wieder diese Kennzahl erhält, was aber bei OR nicht der Fall ist, wie sich zahlenmäßig leicht nachprüfen lässt.

Studie 1	Verumgruppe	Kontrollgruppe	Summe
Erfolg	52,6	10,0	62,6
kein Erfolg	47,4	90,0	137,4
Summe	100	100	200

Studie 2	Verumgruppe	Kontrollgruppe	Summe
Erfolg	97,1	77,0	174,1
kein Erfolg	2,9	23,0	25,9
Summe	100	100	200

Diese zwei Kontingenztafeln liefern jeweils ein OR von 10. Addiert man allerdings die einzelnen Zellen aus, dann ergibt sich die folgende Kontingenztafel mit OR = 3,9:

Studie 1+2	Verumgruppe	Kontrollgruppe	Summe
Erfolg	149,7	87	236,7
kein Erfolg	50,3	113	163,3
Summe	200	200	400

Dieses Beispiel ist sicher extrem, es zeigt aber, dass OR nicht nur schwer zu deuten, sondern als Kennzahl überhaupt wenig geeignet ist. Der einzige Vorteil, den sie ausweist, liegt darin, dass sie größere Zahlenwerte liefert als RD oder RR.

Da selbst formal korrekte Interpretationen der absoluten Werte von Logits (β), genauso wie von Odds Ratios (eβ) uninformativ und potentiell irreführend sind, wird an dieser Stelle empfohlen, lediglich die durch Logits und Odds Ratios implizierte Richtung von Zusammenhängen zu interpretieren.

Interpretation

Aus den genannten Gründen ist ein direkter Rückschluss von einem Zahlenwert für OR auf die Wahrscheinlichkeit des Erfolgs der Therapie nicht möglich. Robert Mathie hat in seiner Meta-Analyse von 2014 für individualisierte Homöopathie zusammengefasst für alle Studien ein OR von 1,53 ermittelt. Was bedeutet das in der Realität für den Patienten, der sich einer homöopathischen Therapie unterziehen will? Man kann allenfalls eine Größenordnung des möglichen Nutzens abschätzen und eine Erfolgsquote für die Placebogruppe (EP) annehmen, vielleicht 20 %, und dann nach der folgenden Formel die Erfolgsquote und den Behandlungserfolg (BE) für die Verumgruppe errechnen:

mit

Selbst wenn man das Ergebnis von Mathie (2014) übernimmt und einmal ignoriert, dass dies nur entstanden ist, weil Studien minderer Qualität einbezogen wurden, die die Ergebnisse in die positive Richtung verfälschen, erscheint das Ergebnis sehr schwach: Für EP = 0,2 und OR = 1,53 ergibt sich Q = 0,383 und daraus wieder BE = 0,077. Also würden weniger als 8 % der Patienten von der Therapie tatsächlich profitieren, mehr als 92 % nicht.

Eine andere Möglichkeit der Interpretation liegt darin, die obige Grafik zu benutzen und daraus abzulesen, dass im günstigsten Fall etwa 10 % der Patienten von der Therapie profitieren – es könnten allerdings auch deutlich weniger sein.

Eine genauere Interpretation von OR ist nicht möglich.

Kontinuierliche Merkmale

Kontinuierliche Daten können im Gegensatz zu dichotomen in einem gewissen Bereich beliebige Werte annehmen, beispielsweise die Körpertemperatur, das Körpergewicht oder auch als Zahlenwert darstellbare Befundergebnisse.

In diesen Fällen würde sich eine Wirksamkeit dadurch zeigen, dass sich die über alle Teilnehmer gemittelten Werte in beiden Gruppen voneinander unterscheiden und die Werte der Verumgruppe in die günstigere Richtung verschoben sind. Die absolute Effektgröße ist dann die Differenz der beiden Mittelwerte. Für Meta-Analysen ist dies jedoch weniger zu gebrauchen, wenn die untersuchten Studien unterschiedliche Zielgrößen mit unterschiedlichen Maßstäben und/oder unterschiedlichen Maßeinheiten verwenden.

Standardized Mean Difference (SMD)

Als dimensionslose Kennzahl wird dann die Standardized Mean Difference („Normierte Differenz der Mittelwerte“) verwendet, die auch nach ihrem Erfinder Cohen's d bezeichnet wird.

SMD wird errechnet, indem die ermittelte Differenz der Mittelwerte beider Gruppen durch die gegebenenfalls gemittelte Standardabweichung der Messwerte beider Gruppen dividiert wird. Die Standardabweichung ist ein Maß dafür, wie stark die einzelnen Werte streuen. Eine kleine Standardabweichung bedeutet, dass die Werte alle dicht beim Mittelwert liegen. Bei einer großen Standardabweichung streuen sie stärker. Obwohl es unterschiedliche Bewertungen gibt (Cochrane Handbook, Kap. 12.6.2), kann man davon ausgehen, dass SMD = 0,2 und kleiner als eine kleine Effektstärke interpretiert wird, 0,5 als eine mittlere und 0,8 und größer als eine große.

Auch SMD stellt eine reine statistische Größe dar, die keine direkten Rückschlüsse auf den Nutzen für den Patienten zulässt. Beispiel: Wenn die Differenz der beiden Mittelwerte der Verum- und der Placebogruppe 2 Maßeinheiten beträgt, dann wäre dies nur ein schwacher Effekt, wenn die Standardabweichung in beiden Gruppen jeweils 10 Maßeinheiten beträgt. Beträgt die Standardabweichung hingegen nur 2,5 Maßeinheiten, dann ist dies ein starker Effekt, obwohl sich für den Patienten fühlbar nichts verändert hat: Die Therapie ist in der Lage, den Befund um zwei Maßeinheiten zu verbessern, ein Effekt, dessen therapeutische Relevanz ganz offensichtlich nicht von der Effektstärke widergegeben wird.

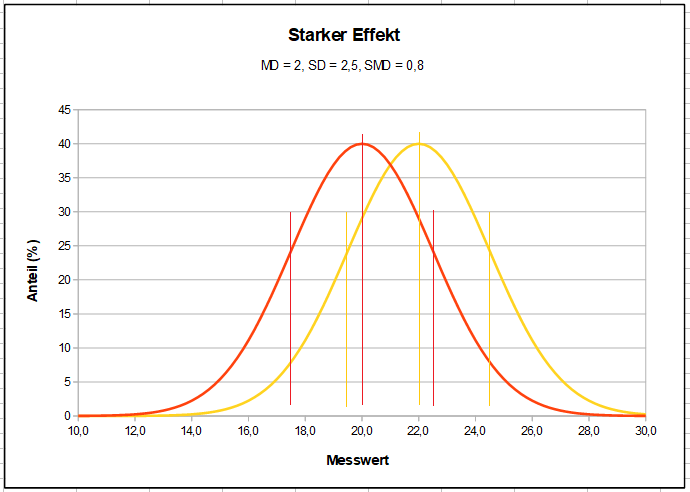
Selbst eine große statistische Effektstärke bedeutet nur geringe Unterschiede in den Ergebnissen, wie im folgenden Diagramm ersichtlich ist: die meisten Patienten werden anhand ihres Therapieerfolges nicht feststellen können, ob sie mit Verum oder Placebo behandelt wurden.

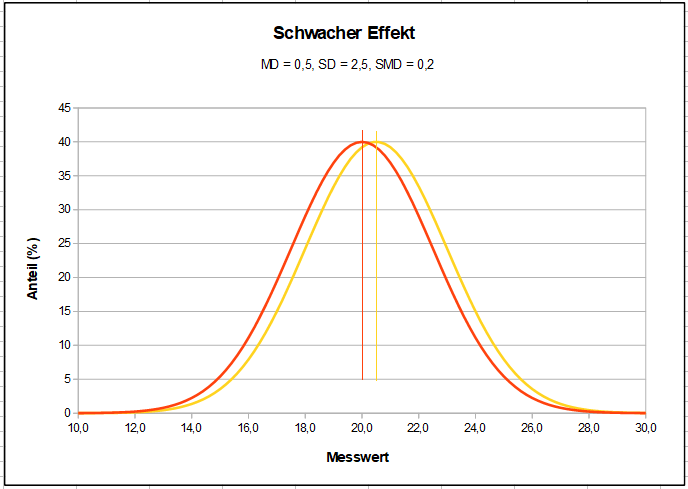
Dieses Diagramm zeigt für hypothetische Zahlenwerte einen „starken Effekt“. Die vertikalen Linien stellen jeweils die Mittelwerte der hier als Normalverteilungen angenommenen Ergebnisse dar, sowie die kürzeren Linien jeweils die Standardabweichungen rechts und links vom Mittelwert. Diese Skizze soll zeigen, wie groß die Überlappung auch bei statistisch starken Effekten noch ist und wie wenige Patienten anhand ihres Befindens klar erkennen können, ob sie Placebo oder Verum erhalten haben. Zum Vergleich hier das Bild eines schwachen Effekts:

Interpretation

Auch hier ist aus den obigen Gründen ein direkter Rückschluss auf einen möglichen Nutzen für den Patienten nicht möglich. Während man bei OR noch einfach mittels eines angenommenen Ausgangswertes für die Placebogruppe die Größenordnung des Effektes abschätzen konnte, ist dies hier praktisch unmöglich, da die Standardabweichung als Bezugsgröße kaum einer auch nur halbwegs zutreffenden Schätzung zugänglich ist. Man kann sich vielleicht anhand statistischer Daten aus der Literatur mit den notwendigen Informationen versorgen, dies ist aber nicht unproblematisch, weil auch zwischen Placebogruppen je nach Zusammensetzung erhebliche Unterschiede bestehen können.

Es gibt allerdings eine Umrechnung von SMD in OR (Cochrane Handbuch Kap. 12.6):

Die genaue Gültigkeit setzt voraus, dass die Daten eine logistische Verteilung bilden, deren Graph auf den ersten Blick eine gewisse Ähnlichkeit mit einer Normalverteilung aufweist, jedoch mathematisch völlig anders aufgebaut ist. Diese Voraussetzung dürfte in der Realität nur in den seltensten Fällen exakt erfüllt sein, weshalb mit diesem Verfahren nur eine grobe Abschätzung möglich ist. Mit dem errechneten OR kann man sich aus der obigen Grafik eine ungefähre Vorstellung verschaffen, was das Ergebnis bedeutet.

Mathie hat in seinem Review aus dem Jahr 2017 zur nicht-individualisierten Homöopathie aus 54 Studien ohne Berücksichtigung der Qualität ein zusammengefasstes SMD von 0,16 ermittelt, das nach obiger Schätzung zu einem OR von 1,37 führt. Wie die Grafik zeigt, proftieren im Maximum nur etwa 8 % der Patienten von der Homöopathie, aber auch nur dann, wenn die Erfolgsquote unter Placebo bei 35 % und mehr liegen würde. Wenn diese Quote hingegen nur bei 20 % liegt, sind es nur 5,5 %. Bei 10 % Erfolgsquote unter Placebo sogar nur noch 3,5 %. Eine wirkmächtige Therapie sollte anders aussehen.

Andere Datentypen

In der Statistik gibt es noch weitere Datentypen, für die auch andere Kennzahlen für die Effektstärke definiert sind. In systematischen Reviews zur Homöopathie werden aber bislang nur dichotome oder kontinuierliche Datentypen verwendet, weshalb auf andere Typen hier nicht eigegangen werden soll.

Zusammenfassung

Die als Ergebnis für systematische Reviews oft angegebene Effektstärke ist wie die Signifikanz eine rein statistische Größe. Dazu ist diese noch sehr schwer hinsichtlich der dahinter stehenden Aussage zu interpretieren. Vermeintlich große Zahlenwerte beruhen oftmals auf eher kleinen Effekten, was nur durch Rückgriff auf die Definition der Kennziffern und auch dann oft nur als grobe Abschätzung erkennbar wird.

Quellen- und Literaturangaben

Anmerkungen und Originalzitate