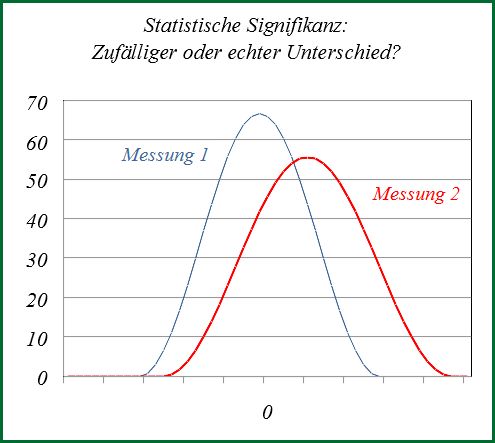
Statistische Signifikanz

Bildquelle:Homöopedia

Die Statistische Signifikanz oder kurz Signifikanz (lat. significare: bedeuten, bezeichnen) ist ein Bewertungskriterium für Ergebnisse, die mit Mitteln der Statistik erzielt wurden. Ein Ergebnis ist dann signifikant, wenn es (sehr wahrscheinlich) nicht auf einem Zufall beruht, sondern (sehr wahrscheinlich) tatsächlich ein realer Effekt aufgetreten ist. Diese Bedeutung weicht von dem Sprachgebrauch im Alltag ab, wo man eher „groß, bedeutend“ mit diesem Begriff verbindet.

Viele wissenschaftliche Ergebnisse beruhen auf der Auswertung von Daten, die sich immer, auch wenn kein äußerer Einfluss aufgetreten ist, mehr oder weniger stark voneinander unterscheiden. Werden zwei Gruppen miteinander verglichen, muss beurteilt werden, ob die Unterschiede auf solchen Streuungen der Messdaten beruhen könnten, also Zufallsprodukte wären, oder nicht. Dazu ermittelt man die Wahrscheinlichkeit dafür, dass die Ergebnisse alleine von solchen Schwankungen verursacht worden sind. Liefert ein für die Art der Daten geeigneter Signifikanztest eine genügend kleine Wahrscheinlichkeit, in der Regel unter 5 %, dann gilt das Ergebnis als signifikant, also nicht als Zufallsprodukt.

Bei klinischen Studien zur Untersuchung der Wirksamkeit von Arzneimitteln werden (mindestens) zwei Gruppen von Teilnehmern miteinander verglichen. In der einen Gruppe wurde das Arzneimittel angewandt, in der anderen nicht. Ist der am Ende der Studie ermittelte Unterschied zwischen den Gruppen wahrscheinlich kein Zufall, dann muss das verabreichte Mittel eine Wirkung entfaltet haben – sofern durch eine geeignete Versuchsführung andere Ursachen ausgeschlossen werden können. Die statistische Signifikanz ist daher eine wesentliche Voraussetzung dafür, dass das Studienergebnis zur Evidenz für die Wirksamkeit des getesteten Mittels beitragen kann. Entsprechend stark ist das Interesse daran, signifikante Ergebnisse zu erzielen.

Dieser Artikel beschäftigt sich mit der statistischen Signifikanz im Hinblick auf Studien zur Homöopathie und setzt sich mit der Bedeutung, Interpretation und auch mit Fehlentwicklungen auseinander. Die mathematisch-statistischen Grundlagen und Rechenverfahren werden nur insoweit behandelt, wie es für die Begründung der abgeleiteten Folgerungen erforderlich ist. Für eine tiefergehende Beschäftigung mit den einzelnen Verfahren sei auf die verschiedenen Lehrbücher zur Statistik verwiesen (Abschnitt Weiterführende Literatur).

Definitionen

Die folgenden Definitionen beziehen sich, sofern nichts anderes gesagt wird, auf klinische Studien, in denen eine Therapie bzw. ein Arzneimittel im Vergleich zu einem Placebo, ein Präparat ohne Wirkstoff, getestet wird. Da es dabei darum geht, die Überlegenheit des Arzneimittels aufzuzeigen, werden solche Untersuchungen als superiority trials bezeichnet.

Im Gegensatz dazu gibt es auch non-inferiority trials, bei denen nachgewiesen werden soll, dass die Wirksamkeit des untersuchten Mittels einem bekannt wirkungsvollen Mittel nicht unterlegen (mindestens gleichwertig) ist. Wegen der unterschiedlichen Zielsetzung gelten die nachfolgenden Beschreibungen für solche Studien nur eingeschränkt.

Statistische Signifikanz

Statistische Signifikanz liegt vor, wenn in einem statistischen Vergleich von zwei oder mehreren Datensätzen die Wahrscheinlichkeit dafür, dass die Unterschiede eine Folge der zufälligen Streuung der Daten sind, unter einem als Signifikanzniveau festgelegten Grenzwert liegt.

Signifikanztest und Nullhypothese

Um eine Wahrscheinlichkeit ausrechnen zu können, geht man von einer als Nullhypothese bezeichneten Annahme aus, die es erlaubt, eine Wahrscheinlichkeit für das Ergebnis zu errechnen, wenn sie denn zuträfe. Etwa: Das verabreichte Mittel hat nicht gewirkt, die Daten der Gruppen unterscheiden sich nur infolge der Streuung.

Dann wird mit einem für die Daten geeigneten Verfahren die Wahrscheinlichkeit für dieses Ergebnis – und alle noch stärkeren Unterschiede – errechnet, wenn die Nullhypothese zuträfe. Liegt dieser Wert unter dem als Signifikanzniveau festgelegten Grenzwert, dann wird angenommen, die Nullhypothese träfe nicht zu, und sie wird verworfen. In diesem Fall wird die Alternativhypothese als gültig angesehen, die den gegenteiligen Sachverhalt ausdrückt.

In klinischen Studien zur Wirksamkeit von Medikamenten wird als Nullhypothese angenommen, dass die Behandlung keine Wirkung hervorgerufen hätte. Genauer: Dass die beiden Gruppen aus der gleichen Grundgesamtheit der Teilnehmer mit bekannten statistischen Daten stammen. Dann wären Unterschiede nur zufällig bei der Aufteilung der Studienteilnehmer auf die beiden Vergleichsgruppen entstanden. Muss diese Annahme zurückgewiesen werden, bleibt die Alternativhypothese bestehen, wonach es nach der Aufteilung (sehr wahrscheinlich) unterschiedliche Einflüsse auf die Gruppen gegeben hat, was die Wirkung des Medikaments nahelegt, sofern andere Einflüsse ausgeschlossen werden können.

In klinischen Studien wird mit einer Vielzahl unterschiedlicher Daten gearbeitet, beispielsweise dichotome Daten (krank vs. nicht krank), Verteilungen kontinuierlicher Daten (Dauer der Symptome), Überlebensdaten und vieles mehr. Entsprechend gibt es viele verschiedene Signifikanztests, Chi-Quadrat-Test, t-Test oder Log-Rank-Test wie in den genannten Fällen. Eine Zusammenstellung der üblichen Testverfahren findet sich in einer Übersichtsarbeit von du Prel et al.

Wie in diesem Abschnitt ersichtlich werden sollte, besteht eine Schwierigkeit in der Interpretation: Es werden Wahrscheinlichkeiten betrachtet, keine absoluten Zahlen und Grenzen. Mithin kann eine einzelne klinische Studie schon aus diesem Grund kein absoluter Beweis sein, denn es ist durchaus möglich, dass das Ergebnis auf einem zwar unwahrscheinlichen, aber eben nicht unmöglichen Zufall beruht, siehe hierzu: Alpha-Fehler.

Signifikanzniveau und Alpha-Fehler

Ein Ergebnis gilt dann als signifikant, wenn die mit einem Signifikanztest ermittelte Wahrscheinlichkeit für den festgestellten Unterschied zwischen den Vergleichsgruppen unter einem bestimmten Wert, dem Signifikanzniveau, liegt. In klinischen Studien wird hierfür üblicherweise ein Wert von 5 % angesetzt, somit gilt eine Wahrscheinlichkeit p < 0,05 als signifikant. Je niedriger der ermittelte Wert p für die Wahrscheinlichkeit, je unwahrscheinlicher das Ergebnis also ist, desto deutlicher spricht es dafür, dass es sich nicht um einen Zufallstreffer handelt, sondern ein Effekt aufgetreten ist. Hier gilt, was vielleicht etwas gewöhnungsbedürftig ist, 'je kleiner desto besser'.

Bei der Bewertung signifikanter Ergebnisse ergibt sich eine Schwierigkeit: Es können Ergebnisse auftreten, die zwar unwahrscheinlicher sind als vom Signifikanzniveau vorgegeben, also als signifikante Ergebnisse erscheinen, aber dennoch durch Zufall hervorgerufen wurden. Man wird also in einem vom Signifikanzniveau vorgegebenen Ausmaß Ergebnisse fälschlicherweise für eine Folge eines aufgetretenen Effekts halten, obwohl sie Zufallsprodukte sind. Dies wird als Alpha-Fehler oder auch als Fehler erster Art bezeichnet, und die Wahrscheinlichkeit für dessen Auftreten ist gleich dem Signifikanzniveau.

Bei dem in klinischen Studien üblicherweise angesetzten Signifikanzniveau von 5 % wird man also in einer von 20 Vergleichsstudien ein Ergebnis, das Zufall ist, für die Auswirkung des Medikaments halten.

Teststärke und Beta-Fehler

Mit der Wahrscheinlichkeit des Signifikanzniveaus tritt ein Alpha-Fehler auf, man hält dann irrtümlich ein Zufallsergebnis für einen eingetretenen Effekt. Andererseits kann es vorkommen, dass es einen Effekt gibt, der aber nicht stark genug ist, um sich als signifikanter Unterschied zu zeigen. Dieser Fehler wird Beta-Fehler oder Fehler zweiter Art genannt. Man hält einen gemessenen Unterschied, weil er nach dem Ergebnis des Signifikanztests mit einer höheren Wahrscheinlichkeit auftreten kann, für ein Zufallsprodukt, tatsächlich aber ist er von einem systematischen Effekt hervorgerufen worden. Bei einer geringen Wahrscheinlichkeit eines Beta-Fehlers spricht man von einer hohen Teststärke oder auch vor statistischer Power (nicht zu verwechseln mit der Effektstärke).

Während man die Wahrscheinlichkeit des Alpha-Fehlers über das Signifikanzniveau einfach festlegen kann, ergibt sich die Teststärke aus Signifikanzniveau, Teilnehmeranzahl und der aufgetretenen Größe des Unterschieds zwischen den Gruppen.

Da sich der Beta-Fehler aus den Daten der Studie ergibt, wird er dazu herangezogen, die Randbedingungen der Studie festzulegen. Dabei strebt man an, für die Wahrscheinlichkeit des Beta-Fehlers den vierfachen Wert der Wahrscheinlichkeit des Alpha-Fehlers zu erreichen, in klinischen Studien daher üblicherweise 20 %, was eine Teststärke von 0,8 ergibt. Das Vorgehen ist also etwa so:

• man wählt ein Signifikanzniveau (5 %)
• man schätzt ab, welche Effektstärke auftreten wird, das heißt, wie groß die festzustellenden Unterschiede der Gruppen voraussichtlich sein werden, wenn das Mittel tatsächlich wirksam ist (alternativ kann man dies auch in einer Pilotstudie ermitteln)
• man bestimmt die für eine ausreichende Teststärke (80 %) notwendige Zahl der Teilnehmer. Die Rechnung wird üblicherweise mit einer passenden Software durchgeführt, z.B. dem Programmpaket G-Power, das im Internet frei verfügbar ist.
  

Wenn es dann gelingt, Daten von hinreichend vielen Teilnehmern zu erhalten, so hat man einen Test, bei dem

• mit einer Wahrscheinlichkeit von 5 % ein Effekt identifiziert wird, obwohl keiner vorliegt
• mit einer Wahrscheinlichkeit von 20 % ein vorliegender Effekt nicht erkannt wird.

Oftmals gelingt es aber nicht, Patienten in ausreichendem Umfang für eine Teilnahme an der Studie zu gewinnen oder es brechen zu viele Patienten die Therapie vor Studienende ab. Dann entsteht eine Studie mit zu geringer statistischer Stärke, was das Risiko erhöhen kann, tatsächlich vorhandene Effekte nicht zu erkennen. Allerdings hat eine zu geringe Teststärke auch Folgen für die Aussagekraft signifikanter Ergebnisse, siehe unter Small Study Bias.

Falsch positiv – falsch negativ

Alpha-Fehler und Beta-Fehler beziehen sich auf die Ablehnung oder Akzeptanz der Nullhypothese, ob dies jeweils zu Recht erfolgte oder nicht. Ein Alpha-Fehler bedeutet, dass man die Nullhypothese verworfen hat, obwohl sie richtig ist. Ein Beta-Fehler hingegen liegt vor, wenn man die Nullhypothese angenommen hat, obwohl sie falsch ist.

Im allgemeinen Gebrauch aber ist es mehr verbreitet, von einem falsch positiven bzw. falsch negativen Ergebnis zu sprechen. Dies ist eindeutig, weil diese Bezeichnungen sich direkt auf die Wirksamkeit des untersuchten Mittels bezieht: Bei einem falsch positiven Ergebnis wurde ein Effekt erkannt, der nicht existiert, bei einem falsch negativen Ergebnis wurde ein tatsächlich vorliegender Effekt nicht erkannt.

Es ist davon abhängig, was als Nullhypothese festgelegt wurde, ob ein falsch positives Ergebnis einem Alpha-Fehler entspricht, obwohl in der Literatur diese Gleichsetzung gelegentlich anzutreffen ist. Für placebokontrollierte Studien trifft das zu, denn in der Nullhypothese wird die Unwirksamkeit des Mittels unterstellt. Bei Studien, bei denen ein Mittel gegen eine andere wirksame Therapie verglichen wird, ist das anders. Dort wird in der Nullhypothese unterstellt, dass das zu prüfende Mittel die gleiche Wirkung hat wie das Vergleichsmittel. Ein Alpha-Fehler wäre dann, dass man die Wirkungsgleichheit ablehnt, obwohl sie in Wahrheit gegeben ist, also ein falsch negatives Ergebnis darstellt.

Signifikanz und Effektstärke

Die Signifikanz ist eine Aussage zur Wahrscheinlichkeit eines festgestellten Effekts, nicht aber zu dessen Größe. Daher ist es irreführend, Studien in der Öffentlichkeit dahingehend zu zitieren, dass signifikante Ergebnisse aufgetreten seien, denn im allgemeinen Sprachgebrauch wird „signifikant“ als „bedeutend“, „herausragend“, „deutlich“ verstanden. Auch aus einem als „hochsignifikant“ bezeichneten Ergebnis folgt nicht zwangsläufig, dass ihm auch ein starker Effekt zugrunde liegt.

Es ist zwar so, dass in einer konkreten Studie eine höhere Effektstärke zu einer besseren Signifikanz führt, jedoch können bei verschiedenen Studien mit der gleichen Signifikanz höchst unterschiedliche Effektstärken aufgetreten sein. Dabei bedeutet eine hohe Effektstärke selbst, so wie sie als statistische Größe auftritt, nicht unbedingt eine hohe therapeutische Relevanz.

Ein Beispiel soll dies verdeutlichen: Es sei hier das Ergebnis aus der Arbeit von Ferley et al. betrachtet, in der die Wirkung des homöopathischen Mittels Oscillococcinum bei Erkältungskrankheiten untersucht wird. Wir betrachten hier die Daten zur Krankheitsdauer aller Patienten, die aus den Angaben der Studie errechnet werden können. Der Einfachheit halber lassen wir für diese Betrachtung die Patienten weg, die innerhalb der Beobachtungszeit von sieben Tagen nicht gesund wurden, denn hierfür wurden in der Arbeit keine Daten angegeben. Dies ergibt die Verteilung im nächsten Bild. Man erkennt die höhere Anzahl der Homöopathie-Patienten, die am zweiten Tag genesen waren.

Genesungsverlauf über der Zeit nach Ferley
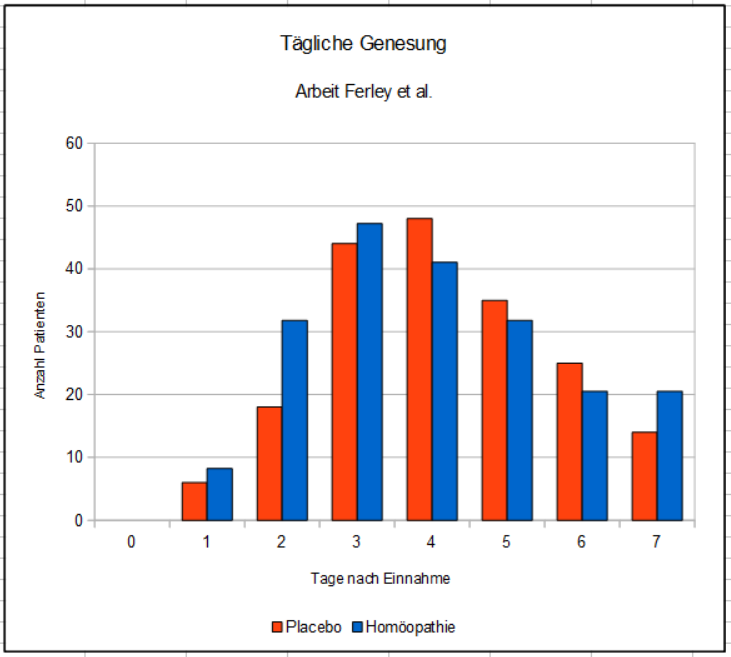
Dargestellt ist die Anzahl der an den einzelnen Tagen genesenen Patienten. Über die Patienten mit einer Genesungsdauer von mehr als sieben Tagen liegen keine Daten vor. Sie sind hier der Einfachheit halber nicht enthalten.
(Diagramm: Homöopedia)

Aus diesen Daten lassen sich folgende statistische Kennwerte errechnen:

	Homöopathie	Placebo
Anzahl Teilnehmer	196	190
Mittlere Dauer (Tage)	3,99	4,27
Standardabweichung (Tage)	1,65	1,45

Die Standardabweichung ist ein statistisches Maß, wie stark eine Verteilung von Daten um ihren Mittelwert streut. Je kleiner dieser Zahlenwert, desto enger liegen die Daten beisammen.

In der Homöopathiegruppe waren die Patienten also im Durchschnitt nur um 0,28 Tage schneller genesen, das sind nur etwas mehr als 7 Stunden. Ein Signifikanztest ergibt mit p = 0,08, dass das Ergebnis nicht signifikant ist. Hätte man den Versuch hingegen mit der doppelten Anzahl Patienten durchgeführt und wären dabei die gleichen Mittelwerte und Streuungen aufgetreten, dann wäre das Ergebnis mit p = 0,012 durchaus signifikant gewesen.

Anmerkung: Der Signifikanztest wurde hier als t-Test ausgeführt, ein Testverfahren, das dafür geeignet ist, statistisch um einen Mittelwert streuende Daten zu vergleichen.

Es sei weiterhin angemerkt, dass es tatsächlich auf einen vorliegenden Effekt hindeuten würde, wenn man den Versuch mit deutlich höherer Teilnehmerzahl durchführen würde und es ergäben sich in beiden Gruppen wieder (in etwa) die gleichen Verteilungen. Aber ob dies tatsächlich der Fall wäre, kann man aufgrund der hier vorliegenden Daten natürlich nicht beurteilen.

Angaben zur Signifikanz

In keiner Studie, in der die Ergebnisse auf statistischem Wege ermittelt wurden, darf eine Angabe zur Signifikanz fehlen, denn dies ist das wesentliche Kriterium, um die Aussagekraft der Arbeit zu beurteilen. Hierfür gibt es mehrere Möglichkeiten.

P-Wert

In vielen, besonders in älteren Arbeiten wird die mittels Signifikanztest ermittelte Wahrscheinlichkeit direkt als Zahlenwert angegeben. Für die Wahrscheinlichkeit wird in der Literatur das Formelzeichen p (oder auch P) verwendet, so dass sich für diese Angabe auch der Begriff P-Wert (oder p-value) eingebürgert hat. Ein Vorteil dieser Angabe ist, dass man direkt erkennen kann, wie deutlich die Signifikanz ausgeprägt ist. Je kleiner der Wert und je weiter vom Signifikanzniveau entfernt – üblicherweise 5 % oder 0,05 – desto besser.

Für das obige Beispiel sähe das Ergebnis beispielsweise so aus: Vorteil zugunsten der Homöopathiegruppe 0,28 Tage, P = 0,08. Üblicherweise wird hierzu noch ein Kennwert für die Streuung angegeben, zumeist der Standardfehler, der hier bei 0,16 liegt.

Vertrauensbereich

Eine andere Möglichkeit, die Signifikanz darzustellen – die auch in neueren Arbeiten bevorzugt wird – benutzt den Vertrauensbereich (auch Konfidenzintervall, KI) des Ergebnisses. Durch die Streuung der Werte wird der an einer Stichprobe ermittelte Messwert nicht dem Messwert der Grundgesamtheit gleichen, sondern je nach Stichprobengröße mehr oder weniger stark davon abweichen („Stichprobenfehler“, „sampling error“). Der Vertrauensbereich ist ein Maß dafür, in welchem Bereich um den Stichprobenmesswert herum der wahre Wert der Grundgesamtheit (wahrscheinlich) liegt.

Anmerkung: Diese Definition des Vertrauensbereichs ist zwar anschaulich, aber nicht exakt richtig. Genau genommen handelt es sich beim Vertrauensbereich um den Bereich, in dem die festgestellten Mittelwerte entsprechend der durch das Konfidenzniveau gegebenen Wahrscheinlichkeit liegen werden, wenn man viele Stichproben aus der gleichen Grundgesamtheit untersucht.

Damit der Vertrauensbereich mit der Signifikanz korrespondiert, wird das Vertrauensniveau als (1 - Signifikanzniveau) festgelegt. Bei einem Signifikanzniveau von üblicherweise 5 % wird also folglich der 95 %-Vertrauensbereich angegeben.

Für die obige Studie kann man errechnen: Vorteil für die Homöopathiegruppe 0,28 Tage, 95 % KI -0,03...0,59. Das bedeutet, dass bei mehrfacher Wiederholung des Experiments 95 % aller Ergebnisse zwischen -0,03 und 0,59 Tagen liegen werden, was vereinfachend dahingehend verstanden werden kann, dass der wahre Wert in der Gesamtbevölkerung auch in diesem Bereich liegen wird. Da der Vertrauensbereich in diesem Fall auch negative Werte umfasst, also möglicherweise tatsächlich ein Nachteil vorliegt, ist das Ergebnis nicht statistisch signifikant.

Für das hypothetische, aber signifikante Ergebnis bei verdoppelter Teilnehmerzahl ergäbe sich ein Vorteil von 0,28 Tagen, 95 % KI 0,07...0,49. Da beide Grenzen im positiven Zahlenbereich liegen, entspricht dies einem statistisch signifikanten Ergebnis.

Beeinflussung der Signifikanz („P-Hacking“)

Für ein Forschungsvorhaben ist es von durchschlagender Bedeutung, ob man ein statistisch signifikantes Ergebnis erzielt hat oder nicht. Daran entscheidet sich, ob das Vorhaben fortgeführt wird, ob Fördergelder fließen, ob die Forschergruppe weiterarbeiten kann – oder eben nicht. Statistisch signifikante Ergebnisse lassen sich leichter publizieren. Auch die persönliche Reputation eines Forschers – was gewissermaßen seinen Marktwert darstellt – hängt davon ab, ob seine Annahmen und Theorien im praktischen Versuch bestätigt werden konnten oder nicht. Signifikante Vorteile können in der Werbung vorteilhaft verwendet werden. Kurz: Signifikanz ist nicht alles, aber ohne Signifikanz ist alles nichts. Entsprechend stark ist auch der Druck, signifikante Ergebnisse zu erzielen – sei es durch ein „Herumfummeln“ mit den Daten, bis statistische Signifikanz erreicht ist, sei es durch den Einsatz zweifelhafter Methoden, die es in erstaunlicher Vielzahl gibt. In der englischsprachigen Literatur hat sich für diese Vorgehensweise der Begriff P-Hacking eingebürgert. Auf Deutsch kennt man den Begriff der Datenmassage.

Das Problem ist sicher nicht nur auf die Homöopathie beschränkt, es findet sich generell in allen Bereichen der Wissenschaft, denn überall sind Menschen tätig, die von den gleichen Motiven angetrieben werden, vor allem sicher von der Überzeugung, dass sie auf dem richtigen Weg sind und nur noch ein kleiner Schritt zum Durchbruch fehlt. Natürlich ist dieses Problem in der Wissenschaft bekannt – und ebenso natürlich versucht man dem Herr zu werden und sicherzustellen, dass die Ergebnisse belastbar sind. Dazu wurde das Problem des P-Hacking sogar wissenschaftlich untersucht.

Viele Studien – sicher nicht nur in der Homöopathie – zeigen Merkmale, die darauf hindeuten, dass ein statistisch signifikantes Ergebnis aufgrund von speziellen Vorgehensweisen zustande gekommen sein könnte, die das Auftreten signifikanter Ergebnisse begünstigen. Aus der Studie kann aber nicht geschlossen werden, dass die Autoren dies willentlich mit dem Ziel eingesetzt haben, ihr Ergebnis signifikant erscheinen zu lassen. Ein gewisser Klärungsbedarf ist sicher gegeben, aber es ist durchaus möglich, dass bestimmte Aspekte in der Veröffentlichung wegen vielleicht mangelnden Problembewusstseins nicht ausreichend beschrieben worden sind oder weil sie als Selbstverständlichkeit erschienen.

Mehrfacher Hypothesentest

Es kann durchaus sinnvoll sein, den mit dem getesteten Medikament zu erzielenden Behandlungserfolg nicht nur anhand eines Kriteriums, sondern anhand mehrerer Parameter zu beurteilen, etwa nach der Dauer der Beschwerden, der Schwere der Symptome, oder auch nach deren Anzahl. Da die Signifikanz eine Wahrscheinlichkeit darstellt, muss bei der Betrachtung berücksichtigt werden, dass es bei mehreren Beurteilungskriterien auch mehrere Chancen für ein signifikantes Ergebnis gibt. Jedes der im Beispiel genannten drei Kriterien hat für sich die Wahrscheinlichkeit, entsprechend des Signifikanzniveaus als falsch positives Ergebnis wahrgenommen zu werden. Die Wahrscheinlichkeit, dass irgendeines der Kriterien als signifikant erscheint, vervielfacht sich folglich um den Faktor der Anzahl der Kriterien. Dieser Effekt wird als Alpha-Fehler-Kumulierung bezeichnet und muss entsprechend korrigiert werden.

Eine einfache Methode ist die Bonferroni-Korrektur, bei der das Signifikanzniveau durch die Zahl der Vergleichsdatensätze dividiert wird. Nur diejenigen Ergebnisse gelten als signifikant, deren Auftretenswahrscheinlichkeit unter diesem Grenzwert liegen. Im obigen Beispiel mit drei Vergleichsdaten müsste die Auftretenswahrscheinlichkeit unter einem Drittel der durch das Signifikanzniveau von 5 % festgelegten Wahrscheinlichkeit erreichen, also p < 0,0167 (1,67 %).

Diese Methode der Korrektur nach Bonferroni gilt als sehr konservativ, das heißt, die Hürde ist sehr hoch und die Gefahr steigt, eigentlich signifikante Ergebnisse nicht als solche zu erkennen. Daher wurden im Laufe der Zeit andere Methoden entwickelt, beispielsweise die Holm-Bonferroni-Korrektur oder das Hochberg-Verfahren.

Wird in der Studie mehr als eine Signifikanzprüfung ausgeführt, dann liegt auch bei p < 0,05 nicht zwangsläufig ein signifikantes Ergebnis vor. Wenn im Text der Studie nicht dargestellt wird, dass eine Korrektur für den mehrfachen Hypothesentest berücksichtigt wurde, dann ist das Ergebnis möglicherweise dennoch nicht signifikant.

Abbrechen bei Signifikanz

Normalerweise wird die Zahl der benötigten Studienteilnehmer anhand der erwarteten Effektgröße und der angestrebten Teststärke festgelegt. Wenn man nun mit jedem neu gewonnenen Datensatz die vorhandenen Daten auswertet, kann es sein, dass sich schon vorzeitig ein signifikantes Ergebnis ergibt, denn der P-Wert ändert sich bei kleinen Teilnehmerzahlen von Datensatz zu Datensatz recht sprunghaft.

Diese Vorgehensweise ist für den Leser der Studien kaum erkennbar, denn es wird eher selten beschrieben, wie die Zahl der Teilnehmer festgelegt wurde. Es kann sehr viele verschiedene Gründe haben, warum an einer Studie nur vergleichsweise wenige Probanden teilgenommen haben. Wenn in der Studie darauf hingewiesen wird, dass die Auswertung erst nach Abschluss der gesamten Datenerfassung durchgeführt wurde, dann ist das ein Hinweis darauf, dass die Studie nicht vorzeitig abgebrochen wurde. Aber sehr häufig fehlt diese Angabe.

Auf die Spitze getrieben wird diese Methode jedoch, wenn nur eine Pilotstudie durchgeführt wurde und dieser auch nach langer Zeit keine Hauptstudie folgt. Pilotstudien dienen dazu, herauszufinden, wie man in einer Hauptstudie am besten vorgeht, und werden mit eingeschränkter Teilnehmerzahl und oftmals ohne klares Zielkriterium durchgeführt. Wenn darauf trotz eines positiven Ergebnisses keine Hauptstudie folgt, dann könnte man darin ebenfalls eine Art P-Hacking sehen, das darin besteht, dass ein eigentlich nicht aussagekräftiges, aber positives Ergebnis einer Pilotstudie nicht weiter geprüft wird – oder womöglich geprüft, aber das Ergebnis nicht veröffentlicht worden ist.

Von den 32 Studien, die Mathie et al. in ihrer 2014 veröffentlichten systematischen Übersichtsarbeit betrachtet hatten, handelte es sich bei zehn um solche Pilotstudien, denen im Maximum auch nach 20 Jahren noch keine Hauptstudie gefolgt ist. Sogar bei zwei der drei als „belastbare Evidenz“ eingestuften Arbeiten handelt es sich um solche Studien.

Cherrypicking

Beim Cherrypicking („Rosinenpicken“) wird aus den verschiedenen in der Studie ermittelten Vergleichsdaten das im Hinblick auf die Signifikanz vorteilhafteste Ergebnis ausgewählt und im Nachgang („post hoc“) zum Beurteilungskriterium erklärt. Ähnlich wie beim mehrfachen Hypothesentest steigt dadurch, dass man mehrere Ergebnisse probiert, die Wahrscheinlichkeit für ein signifikantes Ergebnis.

In der Realität ist ein Cherrypicking kaum zu erkennen, denn in der Veröffentlichung wird nicht stehen, dass man das Kriterium erst post hoc festgelegt hat, und nur selten wird extra hervorgehoben, dass diese Festlegung korrekterweise vor der Durchführung der Studien erfolgte.

Ein Hinweis, dass kein Cherrypicking oder andere ähnliche Verhaltensweisen vorliegen, wäre eine Pilotstudie, mit der untersucht wurde, anhand welcher Daten man am besten die Wirksamkeit beurteilen kann. Wichtig wäre dabei natürlich, dass die Pilotstudie vor der Durchführung der Hauptstudie veröffentlicht wurde und die Hauptstudie auch die Erkenntnisse aus der Pilotstudie berücksichtigt. Beispielsweise sind die Arbeiten von Jacobs et al. zur Untersuchung homöopathischer Therapien bei kindlichem Durchfall nicht geeignet, diesen Zweifel zu zerstreuen, denn die Pilotstudie wurde erst zwei Jahre nach der Datenerfassung der Hauptstudie veröffentlicht.

Texas Sharpshooter

Sehr ähnlich und nur mit sehr unscharfer Grenze vom Cherrypicking zu unterscheiden ist der Texas Sharpshooter („Texanischer Scharfschütze“). Diesem wird nachgesagt, erst auf ein großes Scheunentor zu schießen und danach die Schießscheibe um die Einschüsse herum zu malen, also das Ziel dem Ergebnis anzupassen. Im Hinblick auf Studienergebnisse bedeutet dies, dass man, ohne vorab ein Zielkriterium festgelegt zu haben, eine Menge Daten erfasst und hinterher aus den aufgetretenen Effekten sein Ziel auswählt. Naturgemäß steigt dabei die Chance, signifikante Ergebnisse zu erzielen.

Es sei an dieser Stelle darauf hingewiesen, dass diese Vorgehensweise für eine Pilotstudie durchaus angemessen ist. Solche Pilotstudien werden – zu niedrigen Kosten mit eingeschränkter Teilnehmerzahl – gerade aus dem Grund durchgeführt, um herauszufinden, welcher Effekt am besten zu messen ist und sich am deutlichsten abzeichnet. Ob dieser Effekt auch tatsächlich vorhanden ist, kann dann erst mit einer nachfolgenden Hauptstudie überprüft werden. Ansonsten kann es sein, dass man eine sich zufällig ergebende Häufung als realen Effekt fehlinterpretiert.

Hinweise für diese Problematik – oder das stark verwandte Cherrypicking – können sein:

• Es gibt keine logisch nachvollziehbare Begründung für ein ungewöhnlich anmutendes Beurteilungskriterium, das sich in der Folge als signifikant erweist.
• Es wurde der Datenpunkt mit den besten Signifikanzwerten unter einer Reihe gleichwertiger Datensätze als Zielkriterium festgelegt.
  

Als Beispiel für den ersten Fall sei die Arbeit von Frass et al. zur homöopathischen Behandlung einer schweren Sepsis angeführt: Das Zielkriterium ist die Überlebensrate nach sechs Monaten, wobei die Überlebensrate nach einem Monat noch kein signifikantes Ergebnis liefert. Es wird keinerlei Erklärung dafür geliefert, wie man vor Beginn der Studie darauf kam, dass die Wirkung weder beim Abschluss der Behandlung, noch einen Monat später, sondern erst nach vollen sechs Monaten eintritt. Es wird nichts angegeben, was begründen würde, dass die Forscher vor Beginn der Studie den für Studien zur Sepsis ungewöhnlich weit entfernten Datenpunkt zu ihrem Beurteilungskriterium erwählt hatten.

In der bereits mehrfach zitierten Arbeit von Ferley et al. zur Behandlung von Erkältungskrankheiten durch Oscillococcinum fällt auf, dass die Genesungsrate bereits am zweiten Tag nach Behandlungsbeginn als Kriterium herangezogen wurde – eine für Erkältungskrankheiten ungewöhnliche Wahl, haben doch absehbar erst sehr wenige Patienten zu diesem Zeitpunkt die Erkältung überwunden. Dies war allerdings die einzig mögliche Wahl eines Kriteriums, bei der ein signifikantes Ergebnis erzielt werden konnte. Bereits einen Tag später wäre der Unterschied nicht mehr signifikant gewesen.

Jacobs beurteilt den Erfolg der homöopathischen Behandlung von kindlichem Durchfall am dritten Tag nach Beginn, als die Beschwerden durchaus noch vorhanden waren – an jedem anderen Tag hätte sich allerdings kein signifikantes Ergebnis ergeben, an Tag 4 war der Vorsprung der Homöopathiegruppe praktisch aufgezehrt.

Data Mining

Data Mining („Daten-Bergbau“) ist eigentlich ein wichtiges wissenschaftliches Verfahren. Es dient dazu, Effekte und Zusammenhänge herauszufinden, auf die man durch ein analytisches Vorgehen nicht direkt kommt. Wenn man herausfinden will, welche Erfolge bestimmte gesundheitsorientierte Verhaltensweisen haben könnten (!), dann erhebt man bei vielen Personen eine große Menge an Daten und prüft, welche Daten miteinander korrelieren, also zusammen auftreten und sich in einer charakteristischen Weise zusammen ändern. Hierzu gibt es mächtige Analysetools, die große Datenmengen dahingehend untersuchen können. Solche Korrelationen sind Ausgangspunkte für eine weitergehende Forschung, in der bestätigt oder widerlegt werden muss, dass der Zusammenhang tatsächlich existiert.

Bei klinischen Studien ist mit dem Begriff Data Mining ein ähnliches Vorgehen gemeint, bei dem ebenfalls eine Menge Daten erhoben werden, davon aber nur der Teil Eingang in das Ergebnis findet, der positiv die Hypothese des Autors unterstützt. Die Abgrenzung zum Cherrypicking oder zum Texas Sharpshooter ist naturgemäß fließend. Als wesentliches Merkmal ist hier die große Anzahl der erfassten Messwerte zu sehen.

Ein Beispiel, wie dies aussehen kann, ist die Arbeit von Rottey et al. zur homöopathischen Prophylaxe von Grippesymptomen, d.h. Erkältungskrankheiten. Es wird darin ganz offen berichtet, dass man das Auftreten von acht Grippesymptomen erfasst habe, davon jeweils Häufigkeit und Intensität, also insgesamt 16 Merkmale. Im Ergebnis wird aber nur über drei Symptome berichtet, deren Häufigkeiten in der Homöopathiegruppe signifikant besser waren. Alles andere bleibt im Dunkeln, könnte sich also auch drastisch verschlechtert haben.

Testbasar

Es gibt eine Vielzahl von verschiedenen Testverfahren zur Signifikanz, die für die verschiedensten Arten der untersuchten Daten anwendbar sind. Dabei sind für einen bestimmten Datensatz oftmals mehrere Optionen denkbar. Dann kann man ausprobieren, welcher Test das günstigste Resultat liefert.

Für die Ergebnisse von Ferley sind beispielsweise folgende Tests möglich, wobei die Daten gelegentlich unterschiedlich aufbereitet werden müssen:

• T-Test für die Verteilung der Genesungsdauern, wie in diesem Artikel weiter oben durchgeführt
• Log-rank-Test zum Vergleich des als „Überlebensraten“ aufzufassenden Krankenstands
• Wilcoxon Rangsummentest oder gleichwertig Mann-Whitney-U-Test, in dem die Reihenfolge („Ränge“) bewertet wird, in der die Patienten genesen

Ein ziemlich sicheres Anzeichen, dass die Autoren über den Testbasar gegangen sind und sich ein passendes Verfahren herausgesucht haben, besteht darin, dass ein ansonsten wenig gebräuchlicher Test angewandt wird, obwohl es für die Daten eingeführte Testverfahren gibt.

Schon die Arbeit von Ferley sieht so aus, als hätte man ein passendes Verfahren gesucht. Obwohl es die oben genannten Tests gibt, mit deren Hilfe man die gesamten Daten auswerten könnte, entscheidet man sich dafür, einen Chi-Quadrat-Test auf den Krankenstand an einem bestimmten Tag anzuwenden. In diesem Test werden die Anzahlen der genesenen und noch kranken Patienten beider Gruppen in Beziehung gesetzt.

Papp et al. haben die Arbeit von Ferley et al. wiederholt und die gleiche Art von Daten ermittelt, nämlich den Anteil der noch nicht genesenen Patienten pro Tag. Aber anstatt eines der bekannten und eingeführten Verfahren zu nutzen oder den Chi-Quadrat-Test wie Ferley, verwenden sie einen „Krauth-Test“ zur Signifikanzprüfung, ein Testverfahren also, bei dem man auf erhebliche Schwierigkeiten stößt, im Internet überhaupt eine Verfahrensbeschreibung zu finden. Der Verdacht liegt nahe, dass man lange nach einem Verfahren gesucht hat, das ein signifikantes Ergebnis erbrachte.

Scheinbare Signifikanz

Eher selten wird über ein nicht signifikantes Resultat des Vergleichs der Therapieergebnisse hinweggetäuscht, indem man den Signifikanztest auf andere Weise ausführt als zum Vergleich der Gruppenergebnisse. An sich soll ja in klinischen Studien bewertet werden, ob die aufgetretenen Unterschiede auf eine Wirkung des verabreichten Mittels zurückzuführen sein könnten. Das ist aber offenbar nicht zwingend. Wenn es der Studie weniger um die Suche nach neuem Wissen, sondern mehr darum ging, positiv vermarktungsfähige Daten zu schaffen, kann man das auch anders tun.

In der Arbeit von Cavalcanti werden nicht die Ergebnisse der beiden Gruppen mittels eines Signifikanztests miteinander verglichen, sondern es wird festgestellt, dass sich die Daten in der Homöopathiegruppe im Laufe der Studie signifikant geändert haben. Da fällt kaum auf, dass die Wörtchen „im Vergleich zu“ fehlen. In der Placebogruppe sind auch Verbesserungen eingetreten, nicht ganz so stark wie in der Homöopathiegruppe, aber der Unterschied war nicht groß genug, um am Ende der Studie einen signifikanten Vorteil der Verumgruppe zu erzielen. Wobei ein Signifikanztest, also die Prüfung, ob das Ergebnis auf einem Zufall beruhen könnte, hier karikiert wird. Dass sich die Situation bei aufgetretenen Beschwerden im Laufe einer Therapie bessert, sollte eigentlich kein Zufall sein.

Schönreden der fehlenden Signifikanz

Es kommt häufig vor, dass die Homöopathiegruppe besser abschneidet als die Placebogruppe, sei es, dass mehr Patienten eine Verbesserung ihres Befindens verzeichnen, sei es, dass die Verbesserungen bei den einzelnen Patienten stärker ausgeprägt sind. Häufig geschieht dies allerdings, ohne dass das Ergebnis statistisch signifikant ist. Dies wird oft sehr blumig und wolkig umschrieben.

Sehr häufig wird von einem positiven Trend zugunsten der Homöopathie gesprochen, was aber irreführend ist. Unter Fachleuten dürfte es selbstverständlich geläufig sein, dass hier die Verwendung des Begriffs „Trend“ für „fehlende Signifikanz“ steht. Aber wenn das Studienergebnis in der Öffentlichkeit zitiert wird, dürfte dieser Sprachgebrauch aus Kreisen der Forschung weniger bekannt sein.

Es kann natürlich durchaus sein, dass sich tatsächlich ein positiver Effekt gezeigt hat, der aber wegen der mangelnden Teststärke infolge einer zu geringen Teilnehmerzahl nicht als statistisch signifikant erkannt wurde (Beta-Fehler). Andererseits steigt die Wahrscheinlichkeit dafür, dass das Ergebnis allein aufgrund von Zufällen zustande gekommen ist, wenn P größer wird. Ob im Einzelfall ein Beta-Fehler vorliegt oder ein Zufallsergebnis, ist nicht unterscheidbar.

Demnach ist die Feststellung eines positiven Trends nichts weiter als eine Behauptung, dass es sich nicht um ein Zufallsergebnis handelt, sondern dass es den Effekt, bei dessen Nachweis man gerade gescheitert ist, doch gibt. Dies wäre wiederum nur dadurch nachzuweisen, indem man den gleichen Versuch mit deutlich höherer Teilnehmerzahl, also mit höherer Teststärke, wiederholt.

Konzeptionsgrenzen und Fehldeutungen

Aussagekraft

Obwohl vielfach in der Öffentlichkeit anders zitiert, ist ein signifikantes Ergebnis einer klinischen Studie kein „Beweis“ für eine Wirksamkeit des getesteten Mittels, genauso wenig wie ein nicht signifikantes Ergebnis ein Beweis für das Gegenteil wäre.

Zum einen kennt die Wissenschaft, anders als die Mathematik, keinen Beweis in dem Sinne, dass eine Erkenntnis zutrifft und sich dies auch nie mehr ändern kann. Der Lehrsatz des Pythagoras ist bewiesen und damit ist sicher, dass er für alle Zeiten gültig sein wird. In der Naturwissenschaft hingegen kann jedes als gesichert angenommene Wissen jederzeit durch neuere Erkenntnisse widerlegt werden – was nichts darüber aussagt, wie wahrscheinlich es ist, dass dies auch eintritt.

Das Konzept der Signifikanz hat darüber hinaus einige Schwächen, die bewirken, dass signifikante Ergebnisse auftreten können, auch wenn kein messbarer Effekt vorliegt. Schon weil die Signifikanz bei klinischen Studien ein Grenzwert einer Wahrscheinlichkeit ist, werden 5 % aller an wirkungslosen Mitteln durchgeführten Studien signifikante Ergebnisse aufweisen. Des Weiteren gibt es sehr viele Möglichkeiten, ein signifikantes Ergebnis herbeizuführen, wie die obige Darstellung zeigt.

Zudem sind noch eine ganze Reihe weiterer Irrtümer in Messung, Auswertung und Interpretation der Ergebnisse möglich. Auch ohne böse Absicht wird ein Forscher Ergebnisse, die nicht seiner Hypothese entsprechen, sehr intensiv prüfen und in alle Richtungen hin auf mögliche Irrtümer untersuchen. Für die Überprüfung von Ergebnissen, die wie erwartet und erhofft eingetreten sind, wird wesentlich weniger Energie aufgewendet. Folglich ist bei solchen Ergebnissen eher mit Fehlern zu rechnen.

Schließlich ist die Signifikanz nichts weiter als ein Test, ob sich die Daten nach der Studie durch einen Zufall erklären lassen – und nicht mehr. Aus einem positiven Resultat eines Signifikanztests folgt beispielsweise nicht,

• dass die Nullhypothese tatsächlich unzutreffend ist (s. oben)
• dass das Gegenteil der Nullhypothese bewiesen ist, besonders, wenn dies nicht eindeutig formulierbar ist
• dass ein geeignetes Zielkriterium zur Beurteilung herangezogen wurde
• dass der zugrundliegende Effekt groß und therapeutisch bedeutsam ist
• dass die signifikante Änderung von dem untersuchten Eingriff herrührt
• dass das Ergebnis reproduzierbar ist
• dass ein geeigneter Signifikanztest verwendet und auch sonst korrekt vorgegangen wurde
• dass daraus die richtigen Schlussfolgerungen gezogen wurden

Small Study Bias

Bei kleinen Studien, also Studien, bei denen nicht genügend Patienten rekrutiert werden konnten, um eine ausreichende Teststärke zu erreichen, tritt ein weiteres Problem auf, das als Small Study Bias („Kleine-Studien-Fehler“) bezeichnet wird. Durch verschiedene Einflussfaktoren können hier in besonderem Maße falsch positive bzw. stark in die positive Richtung verzerrte Ergebnisse auftreten:

• Der Anteil der korrekt-positiven Ergebnisse innerhalb der Menge der (vermeintlich) positiven Ergebnisse hängt auch von der Teststärke ab, denn eine mangelnde Teststärke verringert die Anzahl der korrekt-positiven Ergebnisse. In einem Fachgebiet, in dem vorherrschend mit vergleichsweise kleinen Studien gearbeitet wird wie in der Homöopathie (im Schnitt 65 Teilnehmer), ist der Anteil der fälschlicherweise als real bewerteten aber nicht existenten Effekte auf jeden Fall recht hoch – selbst wenn man ignoriert, dass in der Homöopathie ohnehin das Problem der fehlenden a-priori-Wahrscheinlichkeit besteht (s. unten).
• Bei niedrigen Teilnehmerzahlen ist zwangsläufig ein größerer Stichprobenfehler möglich, das heißt, die an der Stichprobe festgestellten Werte können stärker von der Gesamtheit aller Patienten abweichen als bei hohen Teilnehmerzahlen. Andererseits sind bei kleinen Studien große Effektstärken erforderlich, um ein signifikantes Ergebnis zu erzeugen. Demzufolge ist damit zu rechnen, dass die aufgrund kleiner Studien festgestellten Effekte mehr oder weniger stark überzeichnet sind. Dieser Effekt zeigt sich darin, dass einzelne kleine Studien existieren, die aber nicht repliziert werden konnten, denn bei dem vermeintlich festgestellten Effekt handelt es sich um einen zufälligen Ausreißer.

Diese Effekte treten zwangsläufig auf, auch wenn die Autoren absolut sorgfältig und korrekt arbeiten und die Ergebnisse nicht in Richtung positiver Resultate verfälscht werden. Dagegen gibt es weitere Effekte, die eher mit kleinen als mit großen Studien verbunden sind, die Fehldeutungen begünstigen:

• Kleine Studien sind empfindlicher für geringfügige Änderungen in Studiendesign, Auswerteverfahren, Festlegung des Hauptergebnisses und auch Einhaltung der Voraussetzungen für den gewählten statistischen Effekt, auch ohne dass die Autoren dies gezielt beeinflussen. Auch dies führt dazu, dass eine Effektstärke wahrgenommen wird, die real nicht vorliegt und die zu signifikanten Ergebnissen führen könnte.
• Bei kleineren und damit billigeren Studien ist es möglich, dass weniger geschultes und erfahrenes Personal eingesetzt wird. Bei großen und damit teuren Studien ist es wahrscheinlicher, dass auch das Studienprotokoll von mehr und kompetenteren Sachverständigen erarbeitet und überprüft wird. Dies begünstigt bei kleinen Studien eher das Auftreten von Fehlern und Abweichungen, die zu verfälschten Ergebnissen führen können.
• Letztendlich ist auch zu befürchten, dass bei kleinen und billigeren Studien eher als bei größeren auf eine Veröffentlichung verzichtet wird, wenn die Ergebnisse nicht den Vorstellungen entsprechen. Dieser als Publication Bias bekannte Effekt verfälscht die insgesamt vorliegende Evidenz dahingehend, dass für „zu gute“ Studien das Gegengewicht „zu schlechte“ Studien fehlt und Effekte als signifikant angesehen werden, die es nicht oder zumindest nicht in dieser Stärke gibt.

Fehlentwicklungen

Wie kommt es dann, wenn ein signifikantes Ergebnis so wenig aussagt, dass trotzdem so viel Wert darauf gelegt wird, dass die Ergebnisse statistisch signifikant sind?

Ursprünglich war die Signifikanz von ihrem Erfinder Ronald Fisher, einem britischen Statistiker, bei ihrer Einführung in den 1920er Jahren nicht als ein finaler Test gedacht, sondern als ein einfaches Beurteilungskriterium dafür, ob es sich lohnt, die Ergebnisse näher zu betrachten. Dazu führte er die Nullhypothese ein, dass die beiden Gruppen durch den Versuch nicht verändert würden, und errechnete die Wahrscheinlichkeit dafür, das erzielte Ergebnis zu erhalten, wenn das stimmen würde. Dies sollte nur ein Teil einer Bewertung sein, die auch Hintergrundwissen zur wissenschaftlichen Beurteilung einbezog.

Dann hat sich die Signifikanz als augenscheinlich objektives Kriterium für die Beurteilung durchgesetzt, mit fatalen Folgen. Da signifikante Ergebnisse, also vermeintlich reale Entdeckungen, mehr Aufmerksamkeit erzeugen, waren die wissenschaftlichen Journale nur an solchen Ergebnissen interessiert. Da aber auch Null-Effekte mit einer Wahrscheinlichkeit von 5 % signifikante Ergebnisse erzeugen, sind diese in der Literatur überrepräsentiert. Damit geht einher, dass eigentlich nicht existenten Effekten eine gewisse Effektstärke zugeschrieben wird, sonst ergäbe sich ja kein signifikantes Ergebnis. Tendenziell werden positive Ergebnisse als neue Entdeckungen leichter und daher häufiger veröffentlicht als negative („Publication bias“). Die Folge ist, dass der in der Literatur dokumentierte Kenntnisstand der Wissenschaft wahrscheinlich viele Belege für Effekte enthält, die es in Wirklichkeit nicht gibt.

Um wenigstens die Verzerrungen durch den Publication Bias zu vermeiden, wird heute empfohlen, eine Vergleichsstudie vorab registrieren zu lassen, wobei das Studienprotokoll und das Zielkriterium mit festgehalten werden. Es gibt sogar eine Initiative, die die Forderung nach einer gesetzlichen Regelung der vollständigen Registrierung und Erfassung der Ergebnisse als Petition in die verschiedenen Regierungen einbringen will. Entsprechende Register gibt es in mehreren Ländern, unter anderem in USA und der Europäischen Union. Am umfassendsten jedoch ist das Register der Welt-Gesundheitsorganisation (WHO), in dem die Einträge vieler regionaler Register zusammengefasst sind. Hier finden sich auch einige Studien zur Homöopathie. Die Registrierung ist aber bei älteren, vor 2000 veröffentlichten Studien, wie sie in der Homöopathie oft herangezogen werden, nicht der Fall.

Außerdem verzerrt die Konzentration auf die Signifikanz das Denken. Es geht nicht mehr darum, wie groß der Effekt ist, den man entdeckt hat, sondern darum, wie signifikant er ist, was sich in der Öffentlichkeit infolge der Begriffsverschiebung verstärkt. Die Formulierung „Bereits nach zwei Tagen sind signifikante Verbesserungen eingetreten“ klingt viel überzeugender als „Im Mittel ist damit zu rechnen, dass die Dauer der Beschwerden um rund sieben Stunden kürzer ist, wobei das aber unsicher ist, es könnte sich auch um einen Nachteil handeln.“

Vorab-Wahrscheinlichkeit

Alles dies führt dazu, dass Studien mit signifikanten Ergebnissen ganz sicher keine „Beweise“ dafür darstellen können, dass die Homöopathie eine wirkungsvolle Therapie ist und infolgedessen unser Wissen über die Naturgesetze weitestgehend verkehrt oder grob unvollständig sein muss. Dafür sind die in den naturwissenschaftlichen Fachrichtungen mit ausgeklügelten Experimenten der Grundlagenforschung gesammelten Erkenntnisse viel zu gut abgesichert und die klinischen Vergleichsstudien ein viel zu fehleranfälliges Werkzeug. Weil diese aber in der Öffentlichkeit über eine hohe Werbewirksamkeit verfügen, es sich andererseits nach unserem Wissen, wie die Natur funktioniert, nur um falsch positive Ergebnisse handeln kann, ist die Fragestellung nach der Sinnhaftigkeit weiterer klinischer Studien zur Homöopathie durchaus naheliegend.

Eine positive Studie mit einem signifikanten Ergebnis ist eher als Verstärkung oder Bestätigung bereits vorhandener Evidenz zu sehen. In diesem Sinne werden auch in der konventionellen Pharmazie neue Medikamente in kontrollierten Vergleichsstudien getestet, aber nur als ein letzter Baustein in einem mehrstufigen Verfahren.

Dies entspricht dem Gedanken der Vorab-Wahrscheinlichkeit, die eine erfolgreiche Studie verstärken kann. Ausgangspunkt sind etwa folgende Überlegungen: Das Signifikanzniveau gibt die Wahrscheinlichkeit an, dass in Studien falsch positive Ergebnisse auftreten, üblicherweise sind das 5 %. Wenn also von 1000 Studien hypothetisch 900 einen nicht existierenden Effekt untersuchen, dann ergibt dies 45 falsch positive Resultate (5 % von 900). Von den 100 Studien, die einen realen Effekt zum Gegenstand haben, werden wegen des Beta-Fehlers (20 %, siehe oben) nur 80 entdeckt. In diesem fiktiven Fachgebiet stünden am Ende 80 zutreffend-positiven 45 falsch-positiven Effekten gegenüber, es wären also rund ein Drittel der vermeintlichen Entdeckungen falsch (45 von 80+45).

Dreh- und Angelpunkt dieser Betrachtungen ist, wie wahrscheinlich es ist, dass Studien an real existierenden Effekten durchgeführt werden. In der Homöopathie ergibt sich daraus das Problem, dass man aufgrund der naturwissenschaftlichen Unplausibilität nicht von einer Wahrscheinlichkeit für das Vorhandensein eines Effektes ausgehen kann. Dies würde voraussetzen, dass man ein irgendwie plausibles Gedankengebäude angeben könnte, mit dem man einerseits eine Wirkungsweise erklären könnte, das aber andererseits auch nicht mit dem Erkenntnisstand der Naturwissenschaften in krassem Widerspruch stünde. Ohne ein solches Modell kann man keine Wahrscheinlichkeit angeben, mit der die Studien zur Homöopathie reale Effekte betrachten könnten. Als Zahlenwert wäre Null anzusetzen. Damit sind alle angeblich positiven Studien zur Homöopathie als falsche Ergebnisse anzusehen. Diese Argumentation ist jedoch nur bedingt zielführend, denn sie verlagert die Diskussion nur auf die nicht existenten tragfähigen Erklärungsmodelle.

Zusammenfassung

Die Signifikanz eines Ergebnisses ist ein wichtiger Bewertungsmaßstab dafür, ob das erzielte Ergebnis wahrscheinlich auf einem real existierenden Effekt beruht oder eher durch Zufall zustande gekommen ist. Die Interpretation signifikanter Ergebnisse ist aber immer noch schwierig, da es eine ganze Reihe von Umständen gibt, die hier eine Rolle spielen:

• Die Signifikanz ist vom Charakter her eine Wahrscheinlichkeit, kein sicheres Unterscheidungsmerkmal.
• Auch Zufallsergebnisse können im Test als signifikant erscheinen.
• Es gibt viele Möglichkeiten, Ergebnisse bewusst oder unbewusst in Richtung einer Signifikanz zu beeinflussen.
• Die Aussagekraft zu einem therapeutischen Nutzen ist sehr eingeschränkt, obwohl dieser Begriff in der Öffentlichkeit gerade anders verstanden wird.
• Auf keinen Fall stellt ein signifikantes Ergebnis einer klinischen Studie einen festen Beweis für die Wirksamkeit des untersuchten Mittels dar.

Weiterführende Literatur

Lehrbücher zur Statistik im Allgemeinen (Auswahl):

Wissenschaftlich

Bortz J, Schuster C: Statistik für Human- und Sozialwissenschaftler, Springer Verlag, 7. Auflage, ISBN 978-3-6421-2769-4

Bühner M, Ziegler M: Statistik für Psychologen und Sozialwissenschaftler, Verlag der Pearson Deutschland GmbH, München, 2009. ISBN: 978-3-8273-7274-1

Fahrmeir L, Künstler R, Pigeot I, Tutz G: Statistik – Der Weg zur Datenanalyse, Springer Verlag, 7. Auflage, ISBN 978-3-642-01938-8

Rowe P: "Statistik für Mediziner und Pharmazeuten (Verdammt Clever!)", Wiley-VCH Verlag GmbH; Auflage: 1. Auflage (22. August 2012), ISBN 978-3-527-33119-2

Populärwissenschaftlich

Beck-Bornholdt HP, Dubben HH: Der Hund, der Eier legt. Rowohlt, 2001, ISBN 3-499-61154-6,

Quellen- und Literaturangaben